Video: Wat is het nut van logistische regressie?
2024 Auteur: Stanley Ellington | [email protected]. Laatst gewijzigd: 2023-12-16 00:21
Logistieke regressie is de juiste regressie analyse die moet worden uitgevoerd wanneer de afhankelijke variabele dichotoom (binair) is. Logistieke regressie is gebruikt gegevens te beschrijven en de relatie tussen een afhankelijke binaire variabele en een of meer onafhankelijke variabelen op nominale, ordinale, interval- of rationiveau te verklaren.
Mensen vragen zich ook af, wanneer moet logistische regressie worden gebruikt?
Wanneer te gebruiken Logistieke regressie . Jij zou moeten denk na over het gebruik van logistische regressie wanneer uw Y-variabele slechts twee waarden aanneemt. Zo'n variabele wordt "binair" of "dichotoom" genoemd. "Dichotoom" betekent in feite twee categorieën, zoals ja/nee, defect/niet-defect, succes/falen, enzovoort.
Evenzo, wat wordt bedoeld met logistische regressie? Beschrijving. Logistieke regressie is een statistische methode voor het analyseren van een dataset waarin een of meer onafhankelijke variabelen een uitkomst bepalen. De uitkomst wordt gemeten met een dichotome variabele (waarin er slechts twee mogelijke uitkomsten zijn).
Evenzo wordt gevraagd, waar wordt logistische regressie gebruikt?
Logistieke regressie is gebruikt op verschillende gebieden, waaronder machine learning, de meeste medische gebieden en sociale wetenschappen. Bijvoorbeeld de Trauma and Injury Severity Score (TRISS), die veel wordt gebruikt gebruikt om mortaliteit bij gewonde patiënten te voorspellen, werd oorspronkelijk ontwikkeld door Boyd et al. gebruik makend van logistische regressie.
Hoe werkt een logistische regressie?
Gaussische verdeling: Logistieke regressie is een lineair algoritme (met een niet-lineaire transformatie op output). Het doet ga uit van een lineair verband tussen de invoervariabelen en de uitvoer. Gegevenstransformaties van uw invoervariabelen die deze lineaire relatie beter blootleggen, kunnen resulteren in een nauwkeuriger model.
Aanbevolen:
Wat is nut Hoe creëert marketing verschillende vormen van nut?
Utility verwijst naar de waarde of het voordeel dat een klant van de uitwisseling ontvangt, volgens de Universiteit van Delaware. Er zijn vier soorten nut: vorm, plaats, tijd en bezit; samen helpen ze om klanttevredenheid te creëren
Wat is logistische regressie in datamining?
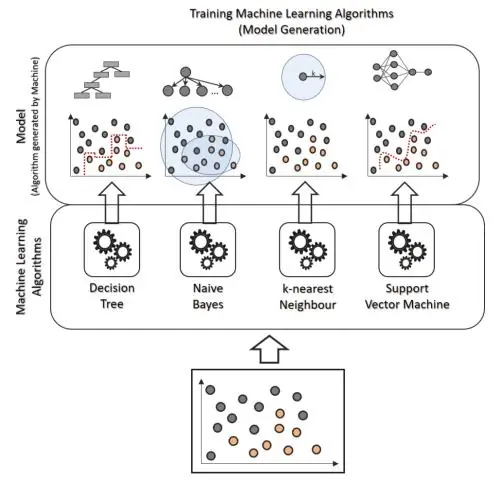
Logistische regressie is een statistische analysemethode die wordt gebruikt om een gegevenswaarde te voorspellen op basis van eerdere waarnemingen van een gegevensset. Een logistisch regressiemodel voorspelt een afhankelijke gegevensvariabele door de relatie tussen een of meer bestaande onafhankelijke variabelen te analyseren
Welke wet is gericht op het verstrekken van sterkere toezichtbevoegdheden, het versterken van het strafrecht tegen terrorisme en het bestrijden van witwassen?
DE PATRIOT ACT VERSTERKT VERSCHILLENDE WETTEN VOOR HET WITWASSEN VAN GELD
Wat is het nut van het circulaire stroommodel?
Het circulaire stroommodel is een economisch model dat de geldstroom door de economie laat zien. De meest voorkomende vorm van dit model is de circulaire inkomensstroom tussen huishoudens en bedrijven. Leden van huishoudens leveren arbeid aan bedrijven via de grondstoffenmarkt
Wat is het belang van het regelen van het koppel bij het aangeven van het instrument?
Het regelkoppel heeft twee functies. Het regelkoppel neemt toe met de afbuiging van het bewegende systeem, zodat de uiteindelijke positie van de wijzer op de schaal overeenkomt met de grootte van een elektrische grootheid (d.w.z. stroom of spanning of vermogen) die moet worden gemeten